Sorting Algorithms (정렬 알고리즘, 파이썬 코드)

Sorting algorithms
며칠전 구글과 전화 인터뷰에서 sorting 알고리즘에 ₩대한₩ 질문을 받았다. 스크리닝이었기 때문에 간단한 질문이었지만 일단 질문을 받았기에, 한번 정리를 해두는 것이 좋을 것 같아 포스팅을 열었다.
구글에 검색해보면 금방 알 수 있듯이 sorting에 여러가지 방법이 있다. 공통적으로 많이 나오는 몇가지 방법을 파이썬 코딩으로 실습해 보고 시간/공간 복잡도가 어떻게 되는지 살펴 보도록 하겠다.
1. Bubble sort
가장 먼저 버블 정렬이 있다. 이것은 바로 옆에 있는 값과 비교하며 원소의 자리를 바꾸며 배열의 끝까지 적용하는 방법이다. 오름차순이라면 둘 중 큰 것을 뒤로 밀면 될 것이고, 내림차순이면 작은 값을 뒤로 밀면 될 것이다.
1-1000 사이의 랜덤 넘버 100개로 이루어진 배열을 하나 만들고 그것을 정렬하는 코드를 짜 볼 수 있다.
아래의 그림은 결과이며 파란색이 정렬 전이고, 빨간색이 정렬 후의 모습이다.
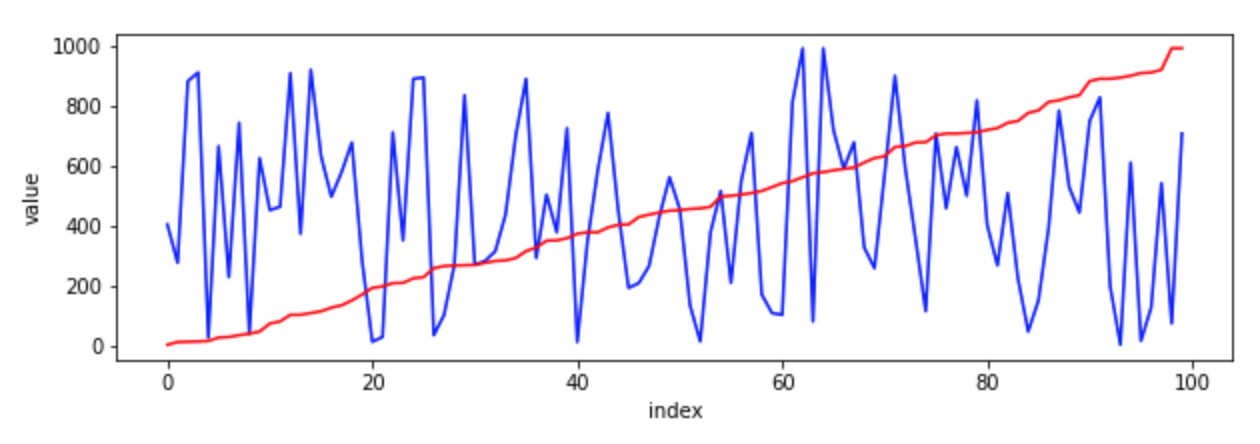
이중 for문을 쓰기 때문에 시간 복잡도는 $O(N^2)$가 될 것이며 공간 복잡도는 배열의 길이만 쓰기 때문에 $O(1)$이다.
Time complexity: $O(N^2)$
Space complexity: $O(1)$
2. Selection Sort
두 번째로 선택 정렬이란 방법이 있다. 이것은 정렬 기준에 맞춰 최소값(내림차순)/최대값(오름차순) 을 뽑으며 정렬하는 것이다. 즉, $N$개의 원소로 이루어진 배열이 주어졌을 때, 처음엔 전체 배열에서 최대값을 뽑고, 두 번째에는 첫 최대값을 제외한 배열에서 다시 최대값을 뽑고, 이런식으로 배열 끝까지 이동하며 정렬하는 방법이다. 버블 정렬 만큼 직관적인 방법이다.

역시 두 개의 for문이 필요하고, 추가적인 공간은 배열의 길이에만 필요하므로 시간/공간 복잡도는 버블 정렬과 같다.
Time complexity: $O(N^2)$
Space complexity: $O(1)$
3. Merge Sort
다음으로는 병합정렬이 있다. 이것은 앞의 두 방법보다는 약간 복잡하다. 병합은 다른 배열을 합친다는 뜻이다. 그렇다면 배열을 나누는 과정이 선행되어야 한다.
그 나누는 방법은 반으로 나누는 것이다. 그 중 첫 번째는 왼쪽 배열(L) 두 번째는 오른쪽 배열(R) 으로 구분한다. 이러한 분리를 recursive(반복적)하게 모든 나눠진 서브 배열 배열의 원소가 하나만 남을때 까지 진행한다. 이렇게 분리를 해놓은 상태에서 바로 옆의 브랜치와 즉, L 과 R의 원소를 비교하며 정렬하고 병합하며 잘라진 배열을 연결하는 것이다.

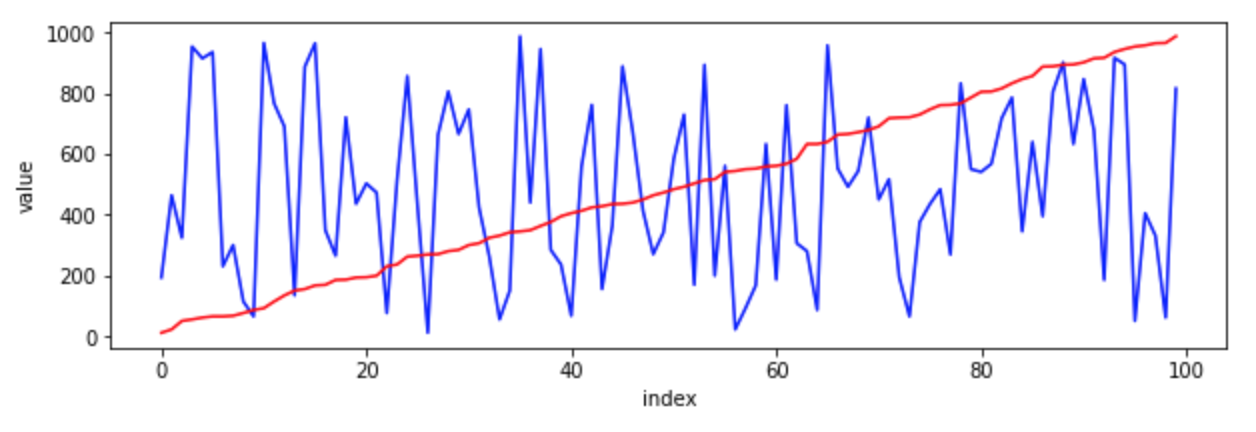
시간 복잡도는 배열의 크기를 반으로 줄여가기 때문에 $N\mathrm{log}N$ 으로 $N^2$보다 감소한다. 하지만 공간 복잡도가 배열의 길이 만큼 늘게 된다. 즉, 메모리를 더 쓰는 대신 시간을 줄이는 것이다.
Time complexity: $O(N\mathrm{log}N)$
Space complexity: $O(N)$
4. Insertion Sort

시간 복잡도는 정렬 전 상태에 크게 의존하기 때문에 범위가 꽤 넓다. 즉 완전히 정렬되어 있는 상태에서 출발한다면 모든 원소를 확인만 하면 되므로 $O(N)$이다. 반면, 정반대로 정렬되어있었다면 $O(N^2)$ 만큼 소요된다.
Time complexity: $O(N) - O(N^2)$
Space complexity: $O(1)$