Image Thresholding(이미지 이진화)
Image Thresholding
이번 포스팅에선 이미지 이진화(image binarization) 대해서 공부해 보도록 한다.
이미지 이진화는 이미지 분리(image segmentation) 을 하는 가장 간단한 방법으로 이미지내의 물체와 배경을 0과 1, 또는 그 반대로, 두 값만으로 픽셀값을 재설정 하는 것이다.
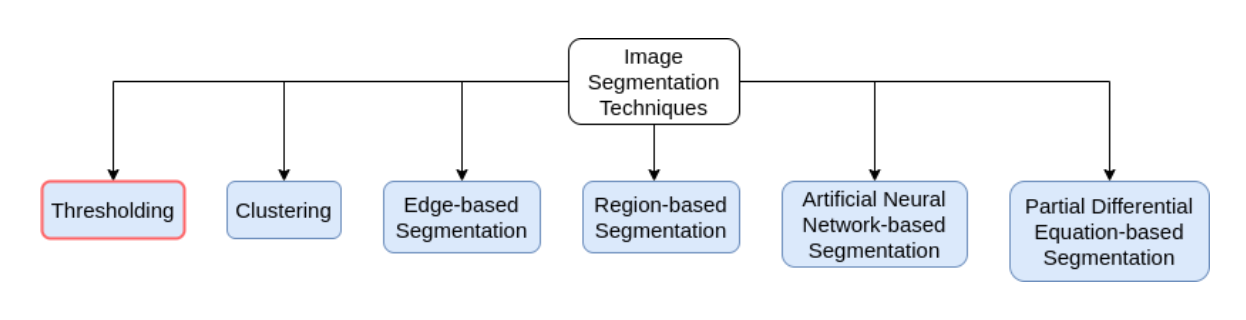
이 방법은 픽셀값이 0~255사이의 값을 가지는 흑백 이미지에만 적용할 수 있다.
픽셀값을 0과 1로 바꾸는 것은 thresh라는 임계값을 기준으로 정해진다.
이 값을 수동으로 주는 것이 기본적인 image thresholding 이며, 자동으로 알고리즘 내에서 정해지도록 하는 방법 중 가장 많이 사용되는 것은 Otus’s method이다.
여기에서 이 두 방법으로 이미지 이진화를 실행해 보도록 하겠다.
Simple image thresholding
image thresholding은 가장 단순하고 간단한 image segmentation 방법이다.
이것을 위해서 분리하는 영역과 배경의 픽셀값을 구분한다. 이것을 이라고 하며, 두 영역을 구분하는 픽셀값을 찾는 것을 뜻한다. 대표적으로 Otsu’s 방법이 있다.
우선 필요한 모듈을 로딩하도록 한다.
그리고 이미지를 읽어 변수에 저장하고 OpenCV의 라이브러리를 이용해서 이진화를 실행해본다.
여기에서 Thresh=0, 최대 픽셀값은 255으로 주었다.

결과에서 보듯이 원본 이미지에는 식별하기 어려웠던 32와 5가 선명하게 보이는 것을 볼 수 있다. 그리고 숫자는 밝기가 255로 배경은 0으로 처리된 이진 이미지 (binary image)가 되었다.
Otsu’s algorithm
Otus 알고리즘은 thresh 값을 사용자 임의로 정하는 것이 아니라, 알고리즘 내에서 자동으로 정해지도록 하는 방법이다.
이 알고리즘의 기본적인 전제는 이미지가 bimodal distribution이라는 것이다. 즉, 이미지 픽셀값들의 히스토그램은 서로 다른 두 개의 픽셀값에서 최대값이 나타는 double peak 분포를 가진다는 것이다.
왼쪽 클래스의 피크는 배경값, 오른쪽 클래스의 피크는 물체의 값일 것이다. 이 두 분포를 가장 잘 나누는 픽셀값을 찾는 것이 이 알고리즘의 핵심이다.
위 전제에 의거해 다음의 수식을 세울 수 있다.
\begin{equation}
\sigma_{T}^2 = \sigma_w^2(t) + \sigma_b^2(t)
\label{eq:totalVariance}
\end{equation}
이것의 의미는 전체 분포의 분산 $\sigma_T$는 두 클래스 내의 (within-class) 분산($\sigma_w$)과 두 클래스 사이의 (between-class) 분산($\sigma_b$)으로 이루어져 있다는 것을 뜻한다.
\begin{equation}
\sigma_w^2(t) = \omega_1(t)\sigma_1^2(t) + \omega_2(t)\sigma_2^2(t)
\label{eq:withinClass}
\end{equation}
the between-class variance is defined as
\begin{equation}
\sigma_b^2(t) = \omega_1(t)\omega_2(t)\left[\mu_1(t)-\mu_2(t) \right]^2
\label{eq:betweenClass}
\end{equation}
이때, 두 클래스의 경계값은 $\sigma_w$을 최소화 시킴과 동시에 $\sigma_b$를 최대화 시키는 값으로 정해진다.
따라서 두 클래스 분포 중 하나만 선택해서 최적화 시키는 thresh값을 찾아내는 것이다. 여기에서는 Eq. \ref{eq:betweenClass} Between-class 분포를 선택하기로 한다.
a. 이미지 로드와 히스토그램 측정
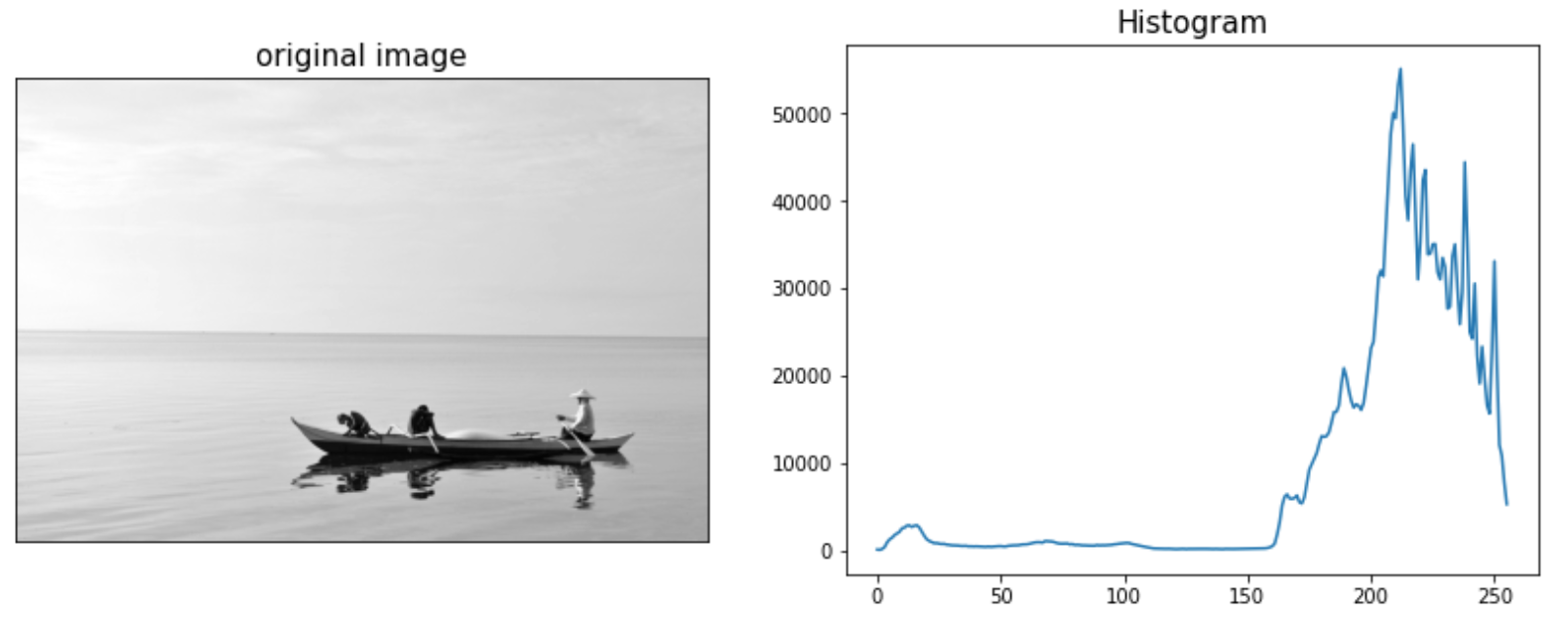
이 알고리즘의 핵심은 이미지의 히스토그램이고, 실행을 위해 새로운 흑백 이미지를 읽고 히스토그램을 만들어본다.
히스토그램에 오른쪽 밝은 값의 픽셀이 많이 있는 것을 알 수 있고 대부분 배경에서 온 것들이다. 반면 우리가 분리해내고 싶은 부분은 배와 그위의 사람들이다. 이 부분은 비교적 낮은 픽셀값들에 해당하며 그 비율은 배경에 비해 아주 낮다.
b. Between-class variance를 최대화 시키는 thresh값 찾기
In Eq. \ref{eq:betweenClass}, the class probability is a cumulative sum. But the sums run in the opposite directions as following
\begin{equation} \omega_1(t) = \sum_{i=0}^{t-1} p(i), \quad \omega_2(t) = \sum_{i=t}^{0} p(i) \label{eq:classProb} \end{equation}
The resulting class probabilities are shown in the left penal below

The means of classes are calculated as following
\begin{equation} \mu_1(t) = \frac{\sum_{i=0}^{t-1} i p(i)}{\omega_1(t)}, \quad \mu_2(t) = \frac{\sum_{i=t}^{0} i p(i)}{\omega_2(t)} \label{eq:classMean} \end{equation}
In figure above, the right penal shows the obtained between-class variance, which appears as a quadratic function and the location of maximum pixel value is the thresh value.
c. OpenCV 내장 함수를 이용해서 얻은 thresh값과 비교
The obtained thresh is about 131.98, which matches well with the one obtained from OpenCV library.
d. 결과

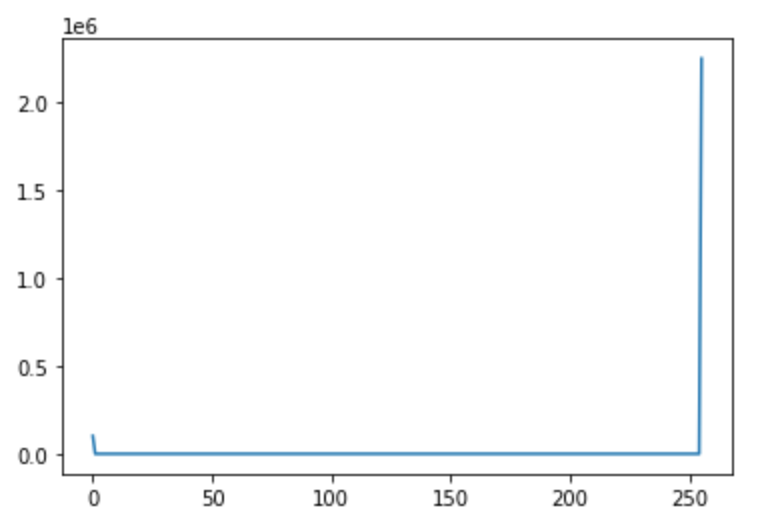
이진화된 이미지의 히스토그램 (histogram of binarized image)
Wrapping it up
이번 포스팅에선 image segmentation의 기초적인 이미지 이진화 처리에 대해서 정리해 보았다. 이 방법은 주로 이미지의 전처리에 해당하며 Computer vision에서 중요한 기초이다.
임계값(thresh) 을 찾아 픽셀값을 나누어 이미지의 픽셀값을 0과 255 두 그룹으로 양분하는 것이 핵심이다.
임계값은 주로 어림짐작으로 줄 수 있는 반면, Otus 알고리즘은 이미지 픽셀값들의 히스토그램을 이용해 자동으로 그 값을 찾는다.
이어지는 포스팅에선 Computer vision에서 아주 중요한 기술인 K-Means Clustering을 이용한 image segmentation에 대해서 공부해 보도록 하겠다.